11.8 Model Comparison with a Quantitative Explanatory Variable

Using the F test to compare models with a quantitative explanatory variable turns out to be a simple extension. As long as we’re talking about thumb length, let’s take the case where Height (measured in inches), a quantitative variable, is used to explain thumb length. We learned in Chapter 8 how to visualize this model, and how to fit the model using lm().

gf_point(Thumb ~ Height, size=4, data=Fingers) %>%
gf_lm(color = "orange")

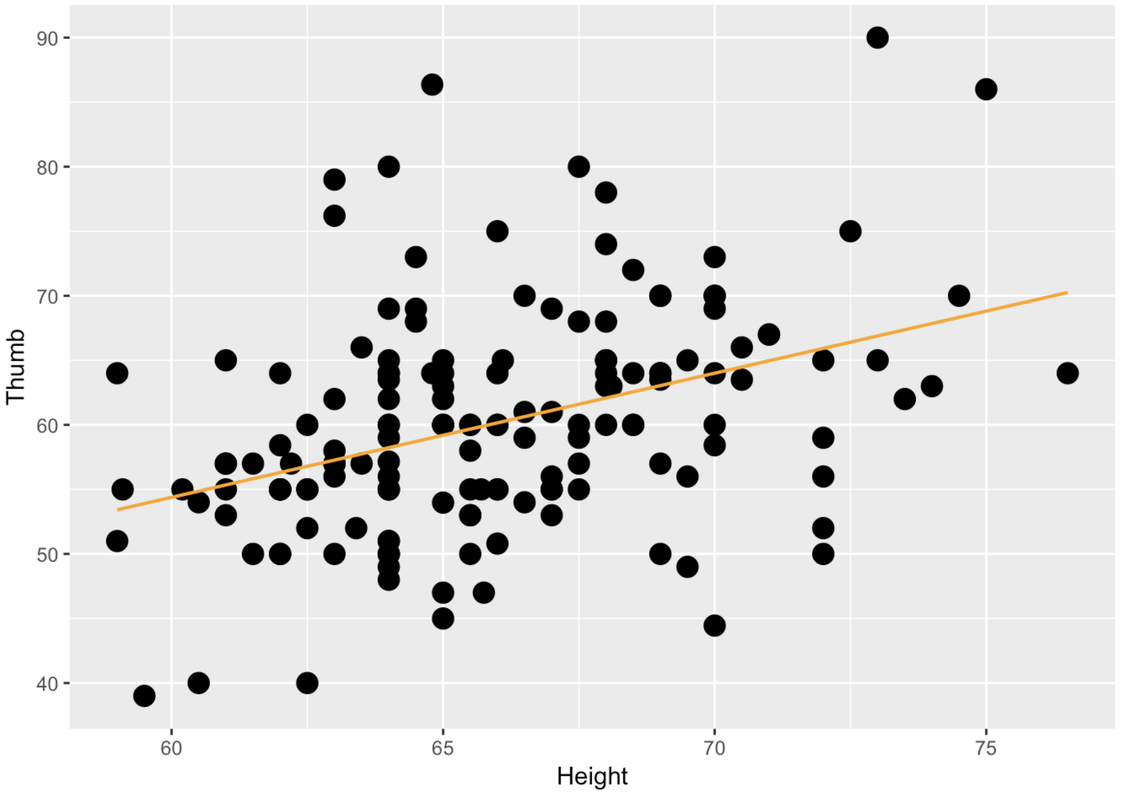
We visualize the relationship between Height and Thumb using a scatter plot, and add the best-fitting regression line to represent the model, \(Y_{i}=b_{0}+b_{1}X_{i}+e_{i}\).

Remember that for Height to explain Thumb, knowing someone’s height would help you make a better guess about their thumb length than if you didn’t know their height. If Height did not explain any of the variation in Thumb (notice the “If..” thinking), we would model it with the empty model (\(Y_{i}=b_{0}+e_{i}\)). Under the empty model, every person’s thumb length would be predicted by the mean of Thumb (and random sampling). We could represent this by simply overlaying a horizontal line on the scatter plot, indicating that no matter your height, we would predict your thumb length as the same: the mean thumb length.

The two scatter plots above show the comparison we want to make. The points are the same in both plots. But the left panel shows the complex model, in which Height predicts Thumb, and the right panel shows the empty model, in which there is no effect of the Height parameter (it’s not even there because it is as if \(b_1 = 0\).)

Randomizing the Sampling Distribution of F

In order to compare these two models, we want to know if the F statistic we observe on fitting the complex model (left) could possibly have occurred by chance if the empty model were true, meaning that there was a zero slope predicting Thumb with Height.

First, let’s find the F value we get by fitting the complex model to our data. We can do this in a number of ways. We can look at the supernova table for the Height.model. We can also use the fVal() function like this:

fVal(Thumb ~ Height, data = Fingers)

We can also use the fVal() function on a model, like this:

fVal(Height.model)

Try using the fVal() function to get the F ratio for the Height model in the code window below.

[1] 27.98408

This seems like a pretty large F value (certainly larger than 4), meaning that it’s very likely we would reject the empty model in favor of our complex model. But just to make sure, let’s see where an F of 27.98 would fall in the sampling distribution if there were, in fact, no effect of Height on Thumb.

We have a couple of ways to get this sampling distribution. One way is to use do(), fVal(), and shuffle() to get a distribution of F values that result from repeated random re-shuffling of our Thumb scores and our Height scores. In other words, by randomly pairing each thumb length in our sample with a height in our sample, and by doing this many times (like 1,000 times), we end up with a distribution of samples that could occur, by chance, if the empty model were true.

Write code to create a randomized sampling distribution of 1,000 Fs (called SDoF) under the assumption that Height has no relationship with Thumb. Print the first six lines of SDoF.

         fVal
1 0.003035482
2 0.002764502
3 0.006996730
4 0.662267009
5 3.695869343
6 0.358804324

Use the code window below to make a histogram of the randomized F ratios.

Above is the randomized sampling distribution of F values that we get from 1,000 re-shufflings of Thumb and Height. It’s pretty obvious that our observed F of 27.98 would be highly unlikely to have occurred just by chance if there were, in fact, no relationship between Height and Thumb. We can check that with the tally() function.

fVal > sampleF
 TRUE FALSE 
    0  1000

If we run tally on our 1,000 randomized Fs, we can see that none of the randomly generated samples had Fs greater than 27.98.

Just for fun, let’s make a sampling distribution with 10,000 shuffled Fs and save it in an R data frame called SDoF10000. Plot those randomized fVals in a histogram.

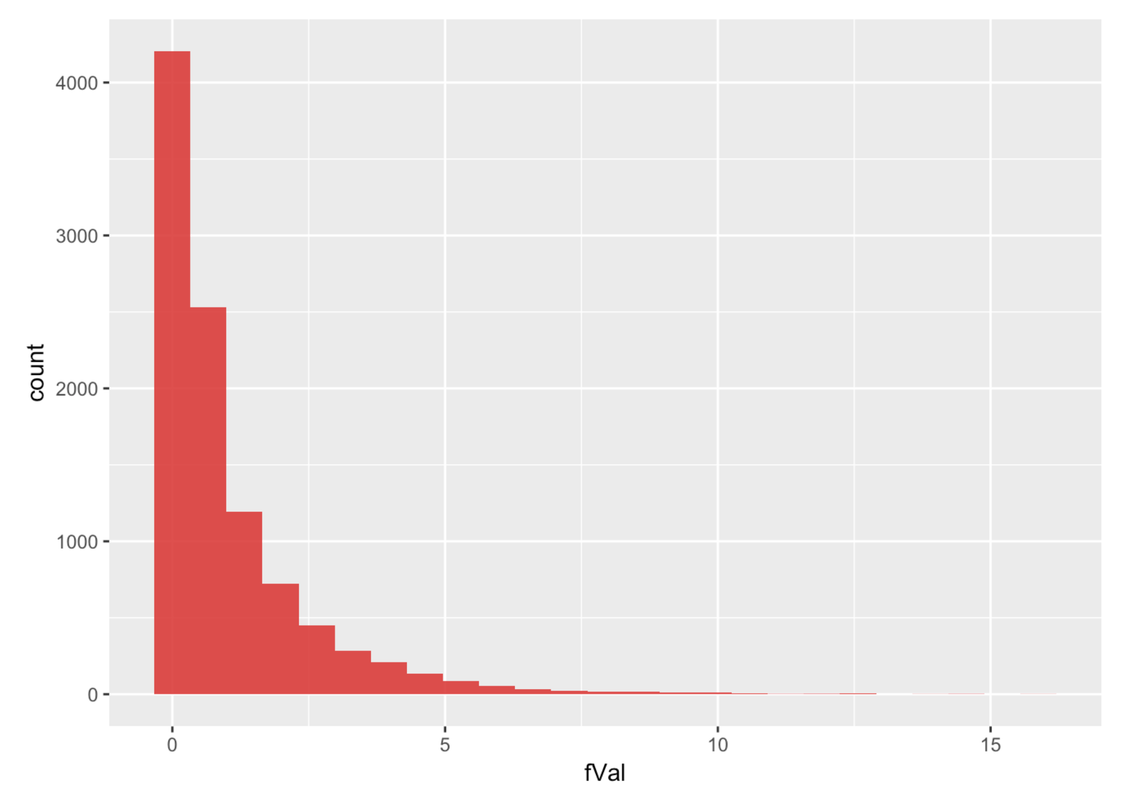
We can see from the histogram of 10,000 randomized Fs that there weren’t any in which samples were as high as the one we observed (27.98). Here is the tally illustrating the same idea.

tally(~ fVal > sampleF, data = SDoF)

fVal > sampleF
 TRUE FALSE 
    0 10000

In both sampling distributions of random re-shuffles (the one with 1,000 Fs and 10,000 Fs), we still did not get a single F larger than the one we observed. When we let the DGP run longer and got more shuffled samples (10,000 iterations), we did get a few extreme Fs (closer to 15), but these were still rare.

You can think of these extreme Fs in these sampling distributions as situations where just by random chance we happened to generate explanatory relationships between the variables. These situations are as if we kept throwing the die 24 times—generating more and more samples—all 24 rolls might come up 6! But that sample is also generated by a random process (just as all the others that “look” more random to us).

From our explorations of randomized Fs, there is very little chance that there is no relationship between Thumb and Height. We surely should reject the simple model in favor of the more complex one.

Relating Hypothesis Testing to Confidence Intervals

As you know by now, we don’t have to randomize to create the sampling distribution of F. We can run supernova() and get the probability of getting an F statistic greater than 27.98 based on the mathematical probability distribution.

supernova(Height.model)

Analysis of Variance Table
Outcome variable: Thumb
Model: lm(formula = Thumb ~ Height, data = Fingers)
 
                               SS  df       MS      F    PRE     p
 ----- ----------------- -------- --- -------- ------ ------ -----
 Model (error reduced) |   1816.9   1 1816.862 27.984 0.1529 .0000
 Error (from model)    |  10063.3 155   64.925                    
 ----- ----------------- -------- --- -------- ------ ------ -----
 Total (empty model)   |  11880.2 156   76.155

We of course get the same F as we get using the fVal() function (it’s our sample F), and that hasn’t changed. The function supernova() only calculates p-value (p stands for probability) to four decimal places. The p-value in the ANOVA table (.0000) means that there is a less than 1 in 10,000 probability of getting an F this high if there is a 0 slope of the line predicting Thumb from Height. That’s pretty much what we found from our randomized sampling distributions of F.

In the code window below, try shuffling to produce a sampling distribution of PREs. How many are greater than our sample PRE?

PRE > samplePRE
 TRUE FALSE 
    0  1000

When we shuffled Thumb length and Height, the resulting Fs and PREs are nowhere near as large as our sample F (27.98) and sample PRE (.15). This suggests that these sample statistics would be difficult to generate from the null model.

If the null model probably did not generate our data, then \(\beta_1\) is probably not 0. If we ran confint(Height.model), we would observe that the confidence interval for \(\beta_1\) would not include 0 and it would be centered around the best-fitting estimate (\(b_1=.96\)). The 95% confidence interval is centered at the best-fitting estimate because the interval extends from the highest \(\beta_1\) that this \(.96\) could have reasonably come from, and the lowest \(\beta_1\) that our sample estimate could have come from.

It turns out that we did this just a chapter ago, so here is the R output for confint(Height.model).

                  2.5 %    97.5 %
(Intercept) -27.0506830 20.391710
Height        0.6026976  1.321069

Just as we predicted, the confidence interval (.60, 1.32) does not include 0 and is centered at .96!

If we know something about the results of the hypothesis test, we can predict something about the confidence interval (CI) around \(\beta_1\). For example, if we reject the null model because the p-value is less than .05, then we know the 95% CI for \(\beta_1\) will not include 0. (Note: The confidence interval is always centered on the sample estimate.) If the null model could have generated our sample, the p-value from hypothesis testing would be greater than .05 and the 95% CI for \(\beta_1\) would include 0.

Knowing the relationship between hypothesis testing and confidence intervals, we could also look at confidence intervals and perfectly predict the result of hypothesis testing.

End of Chapter Survey